Signal processing, communications, and control have traditionally relied on classical statistical modeling techniques utilizing mathematical formulations representing underlying physics, prior information, and additional domain knowledge. These models rely on simplifying assumptions (for example, linear systems and Gaussian and independent noises) to render inference tractable, understandable, and computationally efficient. The simple classical models are useful, but they also are sensitive to inaccuracies and may lead to poor performance when tasked with representing the nuances of real systems displaying high-dimensional complex and dynamic behavior variations.
Approaches which are purely data driven and model agnostic have gained popularity with the abundance of datasets, and the power of modern deep-learning pipelines has increased. The incredible success of deep learning has fueled a general data-driven mindset, but these approaches, too, present limitations. For example, deep neural networks (DNNs) use generic architectures that learn to operate from data and demonstrate excellent performance, especially for supervised problems. However, these DNNs typically require massive amounts of data and immense computational resources, limiting their applicability in various signal processing, communications, and control applications.
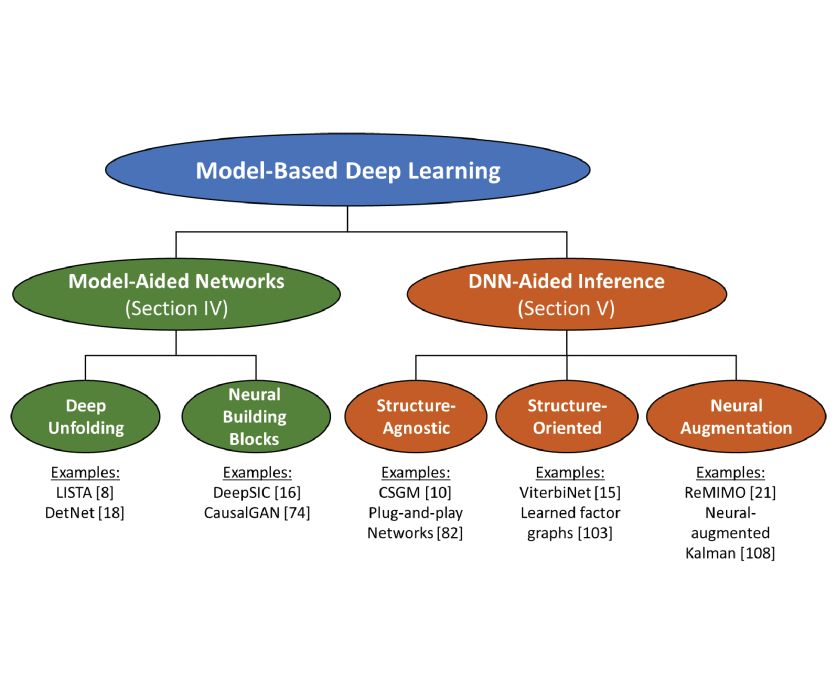
To deliver advantages of both approaches, methods for studying and designing model-based deep learning systems have emerged to combine principled mathematical models with data-driven systems. A multitude of hybrid, application-driven techniques, which are designed and studied in light of a specific task have thus emerged. As shown in an article published by Proceedings of the IEEE, these model-based deep learning methods exploit both partial domain knowledge, via mathematical structures designed for specific problems, and learning from limited data. Among the applications detailed in the article’s examples for model-based deep learning are compressed sensing, digital communications, and tracking in state-space models.
A concrete systematic framework for studying, designing, and comparing approaches is presented in “Model-Based Deep Learning.” Furthermore, possible directions for further research are outlined, including performance guarantees, deep-learning algorithms, collaborative model-based deep learning, and unexplored applications. The article is intended to facilitate the design and study of future systems at the intersection of signal processing and machine learning that incorporate the advantages of both domains.